许久不曾做算法题了,今天的每日一题是道Hard,而我独立地将它搞定了,即便它只有Medium的程度。
实际上是一道没什么意思的题目,本篇主要记录几个思维上的不足点。
题目
给你一个点数组 points 和一个表示角度的整数 angle ,你的位置是 location ,其中 location = [posx, posy] 且 points[i] = [xi, yi] 都表示 X-Y 平面上的整数坐标。
最开始,你面向东方进行观测。你 不能 进行移动改变位置,但可以通过 自转 调整观测角度。换句话说,posx 和 posy 不能改变。你的视野范围的角度用 angle 表示, 这决定了你观测任意方向时可以多宽。设 d 为你逆时针自转旋转的度数,那么你的视野就是角度范围 [d - angle/2, d + angle/2] 所指示的那片区域。
对于每个点,如果由该点、你的位置以及从你的位置直接向东的方向形成的角度 位于你的视野中 ,那么你就可以看到它。
同一个坐标上可以有多个点。你所在的位置也可能存在一些点,但不管你的怎么旋转,总是可以看到这些点。同时,点不会阻碍你看到其他点。
返回你能看到的点的最大数目。
示例1
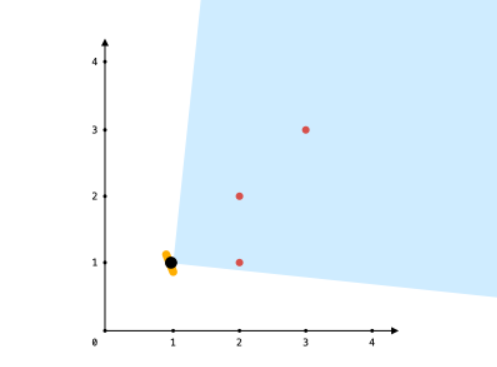
- 输入: points = [[2,1],[2,2],[3,3]], angle = 90, location = [1,1]
- 输出: 3
- 解释: 阴影区域代表你的视野。在你的视野中,所有的点都清晰可见,尽管 [2,2] 和 [3,3]在同一条直线上,你仍然可以看到 [3,3] 。
示例2
- 输入: points = [[1,0],[2,1]], angle = 13, location = [1,1]
- 输出: 1
数据范围
1 <= points.length <= 105points[i].length == 2location.length == 20 <= angle < 3600 <= posx, posy, xi, yi <= 100
分析
根据数据范围,尝试采用 O(nlogn) 的解法即可。
问题转化
在计算可见范围时,我们一定要考虑到的东西不是坐标,而是角度,即 某个点与观测点的夹角 。
对于给定的任意一个点,我们将它作为观测角的 下边 ,然后以这条边为起点,逆时针转 angle 的角度,即可得到观测范围的 上边 ,这样就能得到一个观测范围。
对于这种完全依赖 夹角角度 而不依赖 坐标 的思路,我们应该能够想到 将直角坐标转化为极坐标 。
所谓 极坐标 ,是以观测点为原点,将某点表示为 (ρ,θ) 的形式,即表示为 (极径,极角) 的形式。
这里我们不需要确切知道某个点到观测点的距离,只需要知道它的 极角 ,即它和观测点的夹角,约定以X轴正方向为零度,逆时针增加度数。
因此得到了一个将直角坐标转化为极坐标的函数:
#define PI 3.1415926535897932384626
vector<double> pointsInPolar;
int numberOfSuperpositionPoints;
void changePointsIntoPolar(vector<vector<int>>& points, vector<int>& O)
{
int ox = O[0];
int oy = O[1];
numberOfSuperpositionPoints = 0;
for (auto p : points)
{
int px = p[0];
int py = p[1];
if (px == ox && py == oy)
{
numberOfSuperpositionPoints++;
continue;
}
if (px == ox)
{
if (py > oy)
pointsInPolar.push_back(90.0);
else
{
pointsInPolar.push_back(-90.0);
pointsInPolar.push_back(270.0);
}
continue;
}
// 计算夹角
double pointAngleInPolar = atan2(py - oy, px - ox) * 180 / PI;
pointsInPolar.push_back(pointAngleInPolar);
if (pointAngleInPolar < 0)
pointsInPolar.push_back(pointAngleInPolar + 360.0);
}
sort(pointsInPolar.begin(), pointsInPolar.end());
return ;
}
有几个重点要注意:
- C++函数
atan2用法参见 atan2 - C++ Reference (cplusplus.com) ,它得到的值是 弧度 ,要转为角度(乘180再除以π); - 当给出的点和观测点重合,认为它永远处于视野范围内,用一个变量
numberOfSuperpositionPoints加以记录。 - 当两个点的
X坐标相等,要根据Y坐标的大小判断角度。 - 负数的角度表示从
X轴正方向 顺时针 旋转,那么这种负数角度应该也有正数表示,即加上360°。 - 第三点很重要,并影响到第二点 、
我们可以看到代码中对于负数角度的处理,假如我们有一组数据:
[[0,0],[0,2]]
90
[1,1]
如果放任负数角度不管,我们得到的转化为极坐标的点应该是 [-135.0, 135.0] ,这样,不管以哪个点为视野下边,加上了 90° 的观察角,都无法看到另一个点了。
而按照我们的代码中的处理办法,对于这个负角度的点,我们额外将它的等价正角度点放入了集合中,即应该得到 [-135.0, 135.0, 225.0] 的集合,那么只要以 135.0° 为视野下边,然后加上 90° 的观察角,就能够看到 225° 的点,实际上就是刚才被忽略的负角度的点。
这样做实际上有不小的坏处,那就是 引入额外的空间和时间复杂度 !本来只有一个负角度点,现在要额外存储并计算它的等价正角度点,还是很花费空间和时间的。
但是我今天只是作一个错题的记录,就不考虑它的优化方案了。
求解
现在我们已知视野下边和观察角,相当于也已知视野上边了。要快速从所有点中找到可见点的数目,很简单,做一个二分查找即可。
使用二分查找的办法快速找到 第一个视野上边之上 的点。
int calcVvisiablePointsNumber(int startPointIndex, int visiableAngle)
{
double finalVisiablePoint = pointsInPolar[startPointIndex] + visiableAngle;
int l = 0;
int r = pointsInPolar.size() - 1;
if (pointsInPolar[r] <= finalVisiablePoint)
return r - startPointIndex + 1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (pointsInPolar[mid] <= finalVisiablePoint)
l = mid + 1;
else
r = mid - 1;
}
return l - startPointIndex;
}
我们遍历所有点,分别以它们作为视野下边,用二分求出可见点数,时间复杂度 O(nlogn) 。
AC 代码
class Solution {
private:
#define PI 3.1415926535897932384626
vector<double> pointsInPolar;
int numberOfSuperpositionPoints;
public:
void changePointsIntoPolar(vector<vector<int>>& points, vector<int>& O)
{
int ox = O[0];
int oy = O[1];
numberOfSuperpositionPoints = 0;
for (auto p : points)
{
int px = p[0];
int py = p[1];
if (px == ox && py == oy)
{
numberOfSuperpositionPoints++;
continue;
}
if (px == ox)
{
if (py > oy)
pointsInPolar.push_back(90.0);
else
{
pointsInPolar.push_back(-90.0);
pointsInPolar.push_back(270.0);
}
continue;
}
// 计算夹角
double pointAngleInPolar = atan2(py - oy, px - ox) * 180 / PI;
pointsInPolar.push_back(pointAngleInPolar);
if (pointAngleInPolar < 0)
pointsInPolar.push_back(pointAngleInPolar + 360.0);
}
sort(pointsInPolar.begin(), pointsInPolar.end());
return ;
}
int calcVvisiablePointsNumber(int startPointIndex, int visiableAngle)
{
double finalVisiablePoint = pointsInPolar[startPointIndex] + visiableAngle;
int l = 0;
int r = pointsInPolar.size() - 1;
if (pointsInPolar[r] <= finalVisiablePoint)
return r - startPointIndex + 1;
while (l <= r)
{
int mid = (l + r) >> 1;
if (pointsInPolar[mid] <= finalVisiablePoint)
l = mid + 1;
else
r = mid - 1;
}
return l - startPointIndex;
}
void debugOut()
{
for (auto agl : pointsInPolar)
cout << agl << " ";
cout << endl;
}
int visiblePoints(vector<vector<int>>& points, int angle, vector<int>& location) {
changePointsIntoPolar(points, location);
int res = numberOfSuperpositionPoints;
// debugOut();
for (int i = 0; i < pointsInPolar.size(); i++)
{
int nowVisiablePointNumber = calcVvisiablePointsNumber(i, angle);
res = max(res, nowVisiablePointNumber + numberOfSuperpositionPoints);
}
return res;
}
};
错误记录
In fact,我的代码表现蛮差劲的,但也作为我花费一定时间和脑力独立解决的一道困难题加以记录,仅供自娱自乐罢了。
可以看到我WA了多少次,在此记录一下解题过程中的若干盲区:
- 负角度点没有转化等价为正角度;
- 忽视了“重合点永远可见”这个道理;
- 二分边界。
Over。