题目链接:https://leetcode-cn.com/problems/subarrays-with-k-different-integers/
思路是真难想,想出来之后是真简单。
已经是我目前的水平无法搞定的程度了,在此稍作记录。
题目
给定一个正整数数组
A,如果A的某个子数组中不同整数的个数恰好为K,则称A的这个连续、不一定独立的子数组为好子数组。(例如,
[1,2,3,1,2]中有3个不同的整数:1,2,以及3。)返回
A中好子数组的数目。示例1
输入: A = [1,2,1,2,3], K = 2
输出: 7
解释: 恰好由 2 个不同整数组成的子数组:[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].
示例2
输入: A = [1,2,1,3,4], K = 3
输出: 3
解释: 恰好由 3 个不同整数组成的子数组:[1,2,1,3], [2,1,3], [1,3,4].
数据范围
1 <= A.length <= 200001 <= A[i] <= A.length1 <= K <= A.length
分析
这个月是滑动窗口月啊,这题也想着滑动窗口,但是没有以前的题目那么直白了。
我们可以看看滑动窗口常用的场景——“最值”问题:
在这道题中,我们要把“恰好”转换成为“最多”。使用最多包含
K个不同整数的子区间个数减掉最多包含K - 1个不同整数的子区间个数,正是所要求的恰好包含K个不同整数的子区间个数。为什么能想到这样的思路呢?无他,唯手熟尔。
如何使用滑动窗口求解最多包含K个不同整数的子区间个数呢?我们使用两个指针
left和right来标识一个左闭右闭区间,每当一个窗口满足其内的元素小于等于K个时,这个窗口将会贡献right - left + 1个子数组。当一个窗口内的元素大于K个时,我们移动左指针,使得窗口内的元素再次小于等于K个,然后再考虑它的贡献。为什么一个窗口能贡献这么多的子数组呢?以及这种方法的正确性在哪里呢?
以示例1为例,数组
[1,2,1,2,3], K = 2,我们考虑元素个数小于等于2的所有子数组。当
left = right = 0时,窗口内不同元素个数小于等于2,贡献了一个子数组。当
left = 0, right = 1时,窗口内不同元素个数等于2,贡献了两个子数组。……
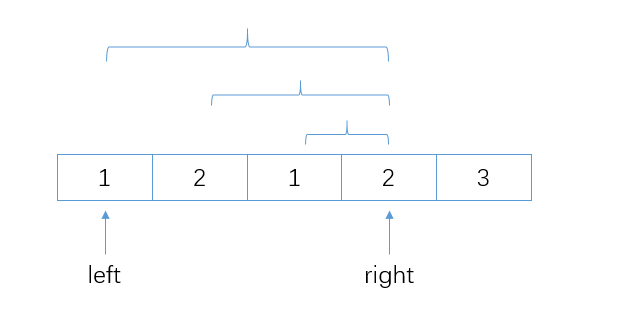
我们特别地考虑
left = 0, right = 3的情况,窗口内不同元素的个数还是2,我们看看它到底是不是贡献了3 - 2 + 1 = 4个子数组。是的,我们从
right向左延伸,包括right所指的元素本身在内,一共能找到right - left + 1 = 4个子数组。注意是从
right向左延伸,因为右边界小于right的子数组一定在更早的循环被考虑过了。比如图中的中间子数组[2, 1],在我们的right = 2时已经考虑过它。因此,能够写出至多包含K个子元素的滑动窗口代码:
int subarrayWithMostKDistinct(vector<int>& A, int K) { int len = A.size(); if (len == 1) return 1; int freq[200001] = { 0 }; int left = 0; int right = 0; int cnt = 0; int res = 0; while (right < len) { freq[A[right]]++; // 加入 if (freq[A[right]] == 1) // 新的元素 { cnt++; } while (cnt > K) // 已经不满足条件 { freq[A[left]]--; if (freq[A[left]] == 0) cnt--; left++; } res += (right - left + 1); right++; } return res; }
AC代码
class Solution {
public:
int subarrayWithMostKDistinct(vector<int>& A, int K)
{
/* 最多包含K个不同元素的子数组个数
` `
*/
int len = A.size();
if (len == 1)
return 1;
int freq[200001] = { 0 };
int left = 0;
int right = 0;
int cnt = 0;
int res = 0;
while (right < len)
{
freq[A[right]]++; // 加入
if (freq[A[right]] == 1) // 新的元素
{
cnt++;
}
while (cnt > K) // 已经不满足条件
{
freq[A[left]]--;
if (freq[A[left]] == 0)
cnt--;
left++;
}
res += (right - left + 1);
right++;
}
return res;
}
int subarraysWithKDistinct(vector<int>& A, int K) {
return subarrayWithMostKDistinct(A, K)
- subarrayWithMostKDistinct(A, K - 1);
}
};
表现效果莫名其妙😏
人一能之,己百之;人十能之,己千之。果能此道矣,虽愚必明,虽柔必强。
参考资料
[1] 力扣(LeetCode).K个不同整数的子数组[EB/OL].2021-02-08