题目链接:https://leetcode-cn.com/problems/swim-in-rising-water/
又是一道不错的复习题,借此回顾回顾BFS和SPFA。
BFS
Breadth First Search,宽度优先搜素。
已知图G = (V, E)和一个源顶点s,宽度优先搜索以一种系统的方式探寻G的边,从而“发现”s所能到达的所有顶点,并计算s到所有这些点的距离(最少边数)。
使用一个数组visited维护每个顶点先前是否被访问过;使用一个数组dist维护源点到每个顶点的距离。visited初始化为全0,dist初始化为全正无穷。
使用一个队列q维护当前正在访问的点,每次从队首中取出head来进行操作。对于head的邻接点tmp,若我们之前没有访问过它,则源点到它的距离就是源点到head的距离加1。我们记dist[tmp] = dist[head] + 1,然后将tmp放入队列q中,之后的某个时刻,tmp会被取出,然后继续找出与它邻接且没被访问过的点,直到队列为空,所有可达的点都被访问过了。
BFS搜索的方法就像那荡开的涟漪,从源点开始不断向外扩张,最终遍历结束,涟漪消散。
使用当年蹭HDU数据结构课的一道作业来进行BFS的回顾:
题目描述
一个迷宫由R行C列格子组成,有的格子里有障碍物,不能走;有的格子是空地,可以走。 给定一个迷宫,求从左上角走到右下角最少需要走多少步(数据保证一定能走到)。只能在水平方向或垂直方向走,不能斜着走。
输入格式
第一行是两个整数,R和C,代表迷宫的长和宽。( 1<= R,C <= 40) 接下来是R行,每行C个字符,代表整个迷宫。 空地格子用’.‘表示,有障碍物的格子用’#‘表示。 迷宫左上角和右下角都是’.’。
输出格式
输出从左上角走到右下角至少要经过多少步(即至少要经过多少个空地格子)。计算步数要包括终点,,不包括起点。如果不能到达右下角,输出“NO”.
输入1:
5 5
..###
#….
#.#.#
#.#.#
#.#..
输出1: 8
这是一道宽搜模板题。从源点出发,向四个方向(上下左右)探寻邻接点,若邻接点合法(即没有越界)且该点不是障碍(’#’)且该点未被访问,则记录它到源点的距离。
我一直不会证明宽搜的正确性,总觉得它理所当然,就直接放代码了:
#include <queue>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
typedef struct {
int x, y;
} Point;
char graph[44][44];
int visited[44][44];
int dist[44][44];
int R, C;
queue<Point> q;
vector<pair<int, int>> dirs = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };
void bfs()
{
Point head;
Point tmp;
// 源点入队
tmp.x = tmp.y = 0;
visited[0][0] = 1;
dist[0][0] = 0;
q.push(tmp);
// 开始宽搜
while (!q.empty())
{
head = q.front();
q.pop();
for (const auto [dirx, diry] : dirs)
{
tmp.x = head.x + dirx;
tmp.y = head.y + diry;
if (
0 <= tmp.x && tmp.x < R && 0 <= tmp.y && tmp.y < C &&
graph[tmp.x][tmp.y] != '#' &&
!visited[tmp.x][tmp.y]
)
{
dist[tmp.x][tmp.y] = dist[head.x][head.y] + 1;
visited[tmp.x][tmp.y] = 1;
q.push(tmp);
}
}
}
}
int main()
{
cin >> R >> C;
for (int i = 0; i < R; ++i)
{
for (int j = 0; j < C; ++j)
{
cin >> graph[i][j];
dist[i][j] = 0xffff;
}
}
bfs();
if (dist[R - 1][C - 1] != 0xffff)
{
cout << dist[R - 1][C - 1] << endl;
}
else
{
cout << "NO\n";
}
return 0;
}
SPFA
终于来到了正题。
SPFA是求单源最短路径的一种算法,其思想与宽搜十分相近。实际上,我当年在完全没有接触此算法的情况下独立地将宽搜改写为了一个粗糙的SPFA,用它通过了一些求最短路的题目。由此可见,在理解宽搜的前提下理解SPFA是比较简单的。
大概还是需要讨论讨论BFS的正确性:我们将当前节点的邻接节点加入队列,由于当前节点到源节点最短,则其邻接节点到源节点也最短。
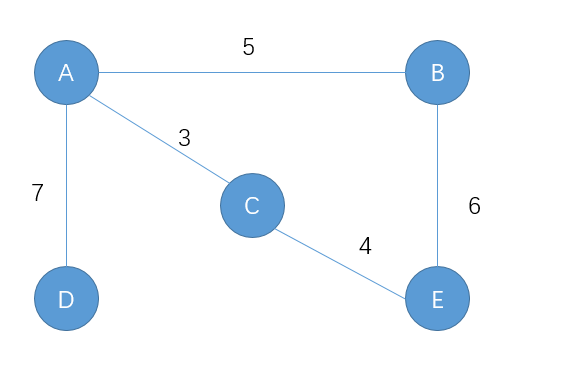
但是,BFS的“距离”实际上是指源节点到当前节点的“跳数”,也就是从源节点出发需要经过几个节点才能到达当前节点。这在一个带权图中是不适用的。考虑以下情况:
我们从源点A出发,到达点E,使用BFS时,情况如下:
- 队列初始只有点A,dist[B] ~ dist[E]都是正无穷,visited[B] ~ visited[E]都是0;
- 点A出队,考虑其所有邻接点B、C、D,设置
dist[B] = 5; dist[C] = 3; dist[D] = 7,并逐一入队,现在队列中有B/C/D;- 点B出队,考虑其所有邻接点E,设置
dist[E] = dist[B] + edge[B][E] = 11;,将E入队,现在队列中有C/D/E;- 点C出队,考虑其所有邻接点E,由于
visited[E] = 1,不再进行更新;- 点D出队,没有邻接点;
- 点E出队,没有邻接点;
- 结束。
可以看到,由BFS最短跳数得到的带权距离并不一定是最短的,而这主要是由于边权具备任意性。实际上,例如在计算机网络中进行路由选路时,路由跳数最少的那条路线也未必是时延最低的,与此例有异曲同工之妙。
在上面的分析中,由visited带来的影响能否消除呢?答案是肯定的。既然可能出现跳数更多但权和更短的路径,那么我们在访问点E的时候考虑其dist[E]和dist[C] + edge[C][E]的大小,令其等于更小的那一个不就可以了吗?
在本例中,这样做确实可以。当点C出队时考虑其邻接点E,由于dist[E] > dist[C] + edge[C][E],我们将dist[E]的值更新为后者,即A到E的最短距离为7。
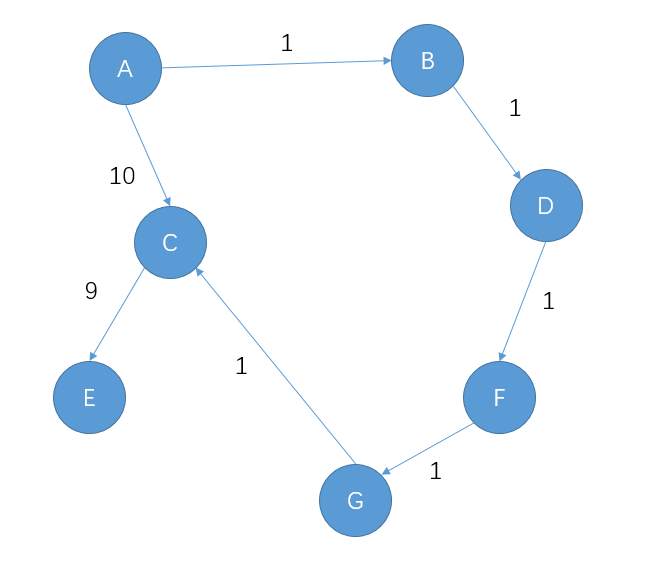
但是,在一个更加复杂的图中,这样做就不完全正确了。考虑这个有向图:
当我们经过了很多跳之后终于找到了一个到达点C的更短路径(A->B->D->F->G->C),发现它的邻接点E早在不知道什么时候就已经用路径A->C->E来计算距离了。
兵来将挡,水来土掩。既然我使用更小的距离来更新某个点时,它的邻接点可能无法得到更新,那么我们干脆让它再次进入队列中,这样之后它从队列中被取出时将会重新更新所有邻接点;同理,被更新的邻接点再次进入队列中,去更新邻接点的邻接点……
没错,SPFA就是如此,且只有如此。
回顾一下说了什么:
- 修改BFS中的距离更新条件,不用visited作为判断标准,而用dist作为判断标准,只要dist更小,就对其进行更新;
- 每次更新了某个点的dist,把它重新入队,这样就能更新它的邻接点。
那么,visited数组就还是有用的:我们之前使用visited来保存访问过的点,BFS过程中遇到访问过的点就不再访问了;现在可以使用visited来保存一个点是否存在队列中,若是,我们更新它的dist的时候就不用入队,因为它本来就在队列里面。采用这个办法,每次一个点出队的时候就将对应的visited设置为0,为其提供再次入队的可能性。
说了那么多,看看LeetCode778. 水位上升的泳池中游泳:
在一个 N x N 的坐标方格 grid 中,每一个方格的值
grid[i][j]表示在位置(i,j)的平台高度。现在开始下雨了。当时间为
t时,此时雨水导致水池中任意位置的水位为t。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。你从坐标方格的左上平台 (0,0) 出发。最少耗时多久你才能到达坐标方格的右下平台
(N-1, N-1)?示例1
输入: [[0,2],[1,3]]
输出: 3
解释: 时间为0时,你位于坐标方格的位置为 (0, 0)。 此时你不能游向任意方向,因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时,你才可以游向平台 (1, 1). 因为此时的水位是 3,坐标方格中的平台没有比水位 3 更高的,所以你可以游向坐标方格中的任意位置
这道题可以使用变相的SPFA来解决。我们的dist不再是源点到任一点的距离,而是源点到达任一点所需要的时间。对于一个点的邻接点,如果自己的高度比它高,则说明我们到达当前这个点的时候,水面已经没过了这个邻接点;如果自己的高度比它低,说明我们到达当前这个点的时候还没办法到达邻接点,因为至少需要等待水面没过它;所以采用当前这条路径,要到达这个邻接点的时间就是max(grid[tmp.x][tmp.y], distance[head.x][head.y])。
那么根据SPFA的逻辑,就能得到如下的代码:
class Solution {
public:
typedef struct {
int x, y;
} Point;
int swimInWater(vector<vector<int>>& grid) {
const int n = grid.size();
int visited[51][51] = { 0 };
int distance[51][51];
vector<pair<int, int>> dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
distance[i][j] = n * n;
}
}
// SPFA
queue<Point> q;
Point head;
Point tmp;
tmp.x = tmp.y = 0;
distance[0][0] = grid[0][0];
q.push(tmp);
visited[0][0] = 1;
while (!q.empty())
{
head = q.front();
q.pop();
visited[head.x][head.y] = 0; // 提供再次入队的可能性
for (const auto [dirx, diry] : dirs) // 对于所有邻接点
{
tmp.x = head.x + dirx;
tmp.y = head.y + diry;
if (
(0 <= tmp.x && tmp.x < n) &&
(0 <= tmp.y && tmp.y < n) &&
distance[tmp.x][tmp.y] >
max(grid[tmp.x][tmp.y], distance[head.x][head.y])
)
{
distance[tmp.x][tmp.y] =
max(grid[tmp.x][tmp.y], distance[head.x][head.y]);
if (!visited[tmp.x][tmp.y])
{
q.push(tmp);
visited[tmp.x][tmp.y] = 1;
}
}
}
}
return distance[n - 1][n - 1];
}
};
表现一般,主要是由于SPFA算法在稀疏图的情况下表现更好,在这种稠密图中时间复杂度退化了。
这题实际上还是使用Dijkstra算法会好一些,官方还提供了二分答案(思路简单!)、并查集等骚操作,不在本文的讨论范围内。
参考资料
[1] 力扣官方题解.水位上升的泳池中游泳[EB/OL].2021-01-30
[2] SHHHS.SPFA算法[EB/OL].2016-09-14
https://www.cnblogs.com/shadowland/p/5870640.html
[3] 360百科.宽度优先搜索[EB/OL]