题目链接：https://leetcode-cn.com/problems/non-decreasing-array/
看到这题第一感受：简单题！
做完这题第一感受：简单题？
题目
给你一个长度为
n的整数数组，请你判断在 最多 改变1个元素的情况下，该数组能否变成一个非递减数列。我们是这样定义一个非递减数列的： 对于数组中所有的
i(0 <= i <= n-2)，总满足nums[i] <= nums[i + 1]。示例1
输入： nums = [4,2,3]
输出： true
解释： 你可以通过把第一个4变成1来使得它成为一个非递减数列。
示例2
输入： nums = [4,2,1]
输出： false
数据范围
1 <= n <= 10 ^ 4- 10 ^ 5 <= nums[i] <= 10 ^ 5
分析
简单题毕竟还是简单题，思路初步找起来是比较容易的。
我们把所有元素以
(index, value)这种形式在坐标轴上画出来，横坐标是元素下标，纵坐标是元素数值，那么如果希望该数组是一个非递减数列，这张折线图的形状最终需要满足各个部位的斜率都大于等于0。如果在允许改变一个元素的情况下，希望该数组变为一个非递减数列，那么初始图形只允许有一个波谷存在，而且这个波谷还必须具备某些性质。
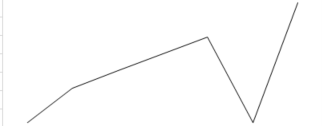
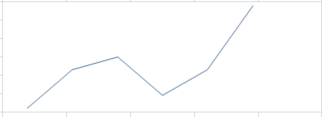
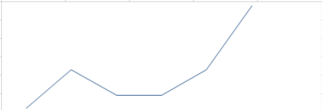
例如，对于一组数据
3,5,6,7,8,3,10，可以改变倒数第二个元素3，令其等于8，即可构成一个非递减数列。这组数据原本的折线图是这样的：
Fig 1. 改变一个元素后的折线图是这样的：
Fig 2. 下面给出原始折线图需要满足的两个性质：
对于原始的折线图，首先只允许有一个波谷存在，如果超过一个波谷，说明存在有两处的非递减情况，这时只改变一个元素是不行的。
对于这一处波谷，还有几种情况：
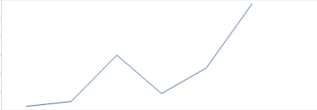
波谷左边的元素小于等于波谷右边。也就是
Fig1的情况，我们可以直接令波谷元素等于波谷左边的元素，这样就填平了波谷，并且保持继续上涨的趋势不变；如果波谷右边已经没有元素，说明已经到达了最后，直接将波谷元素拔高即可；波谷左边的元素大于波谷右边。此时我们就不能将波谷拔高到其左边的元素了，只能将其左边的元素拉低到波谷。这种情况下，我们要考虑到波谷左边第二个元素，如果它也大于波谷，这时就不存在一种办法来填平波谷。
我们先看看可以填平波谷的情况：
Fig 3. 可以看到，波谷左边第二个元素小于波谷，那么我们将波谷左边的元素拉低到波谷的水平，就能把波谷消除掉：
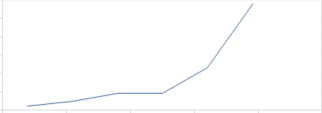
Fig 4. 当波谷左边第二个元素大于波谷，我们把波谷左边的元素拉低到波谷时，产生了新的波谷：
波谷左边第二个元素大于波谷
产生新的波谷 特别地，当波谷左边只有一个元素，自然就直接将左边的元素拉低即可。示例1中的
nums = [4,2,3]就属于这种情况。
AC代码
下标从前往后递增，每次判断是否出现一个下降的区段。
首先，全局范围内只能出现一次下降；
其次，这个波谷要分上面两种情况讨论。
class Solution {
public:
bool checkPossibility(vector<int>& nums) {
int len = nums.size();
if (len == 1)
{
return true;
}
int ptr;
int change = 0; // 改变的元素个数
bool res = true;
ptr = 1;
while (ptr < len)
{
if (nums[ptr] < nums[ptr - 1]) // 递减了
{
if (change < 1)
{
// 波谷左边的元素大于波谷右边，只能拉低左边元素，不能拔高波谷
if (ptr + 1 < len && nums[ptr - 1] > nums[ptr + 1])
{
// 只能改变nums[ptr - 1]
if ((ptr - 2 >= 0 && nums[ptr - 2] <= nums[ptr]) || ptr == 1)
{
nums[ptr - 1] = nums[ptr];
change++;
continue;
}
else
{
// nums[ptr - 2] > nums[ptr]
res = false;
break;
}
}
else // 波谷左边元素小于等于波谷右边元素，直接拔高波谷
{
nums[ptr] = nums[ptr - 1];
change++;
continue;
}
}
else
{
res = false;
break;
}
}
ptr++;
}
return res;
}
};
表现很一般，就不放出来了。比较复杂的逻辑增大了时间消耗，暂时没有看到有什么优化的办法。