难题本为数不多的Hard题~
题目
给你一个 m x n 的矩阵 matrix 和一个整数 k ,找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。
题目数据保证总会存在一个数值和不超过 k 的矩形区域。
示例1
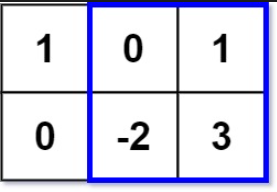
- 输入: matrix = [[1,0,1],[0,-2,3]], k = 2
- 输出: 2
- 解释: 蓝色边框圈出来的矩形区域
[[0, 1], [-2, 3]]的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。
示例2
- 输入: matrix = [[2,2,-1]], k = 3
- 输出: 3
数据范围
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-100 <= matrix[i][j] <= 100-105 <= k <= 105
分析
我们要得到每一个小矩形,则可以:
- 遍历上下界
- 遍历左右界
只分析遍历上下界的情况,当我们得到了一组确定的上下界之后,我们可以得到很多个矩形区域:
可以看到,这个矩形区域由给定的上下界和 几个连续的列 组成。
在这个矩形区域中,我们的总和不能超过 k 。只要我们求出每一列的总和,则可以将原问题转化为:
给定一个整数数组和一个整数 k,计算该数组的最大区间和,要求区间和不超过 k。
问题一、 如何快速求出每一列的总和呢?
我们在最外层遍历上边界,对于递增的下边界来说,只需要在上一轮的结果中加上当前这一行的元素,即可得到每一列的总和。
问题二、 如何快速求出不超过 k 的区间和呢?
区间和不超过 k ,转化为公式如下:
对于区间 s 、区间右端 r 和区间左端 l ,使得
prefix_sum[r] - prefix_sum[l - 1] <= k。
我们使用了前缀和 prefix_sum ,且区间左右都是闭合的。
在本题中,我们可以从左向右遍历,计算出新的前缀和 prefix_sum[r] ,同时,我们使用一个 有序集合 保存以前计算过的所有前缀和即 prefix_sum[0 ~ l] ,从集合中快速查找是否存在一个元素满足上面的式子即可。
说到有序集合,不得不提 set ,原式可以变化为 prefix_sum[l - 1] >= prefix_sum[r] - k ,即我们要找的元素正是 set.lower_bound(prefix_sum[r] - k) 。
AC代码
class Solution {
public:
int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
int upper, lower;
int row = matrix.size();
int col = matrix[0].size();
int ans = INT_MIN;
for (upper = 0; upper < row; upper++)
{
vector<int> col_sum(col);
for (lower = upper; lower < row; lower++)
{
for (int c = 0; c < col; c++)
{
col_sum[c] += matrix[lower][c];
}
int right = 0;
set<int> s = { 0 };
set<int>::iterator left;
// for each right-pos
for (int r = 0; r < col; r++)
{
// right --> prefix_sum[r]
right += col_sum[r];
// right - left <= k
// left >= right - k
left = s.lower_bound(right - k);
if (left != s.end())
{
ans = max(ans, right - *left);
}
s.insert(right);
}
}
}
return ans;
}
};
在上面的代码中,注意:
- 每列的和
col_sum是固定了上边界之后才开始计算的,故变量定义在第一层循环内;- 有序集合初始需要一个
0,否则计算前缀和的时候无法考虑prefix_sum[r]本身;
参考资料
[1] 力扣官方题解.矩形区域不超过 K 的最大数值和[EB/OL].2021-04-21