题目链接:https://leetcode-cn.com/problems/reverse-bits/
一道简单题,却能引出一个无比骚包的操作。此法前所未见,独自亦难想出,因此大抵也算是难的。
题目
颠倒给定的 32 位无符号整数的二进制位。
示例1
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596, 因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例2
- 输入: 11111111111111111111111111111101
- 输出: 10111111111111111111111111111111
分析
易得简单暴力的32次循环法,在此不表,详见AC代码1。唯有一点值得注意:先加最低位再将
res移位的时候,只能移动31次,否则最高位将溢出。因此,AC代码1中只取31次循环,而将最后一位置于循环外。
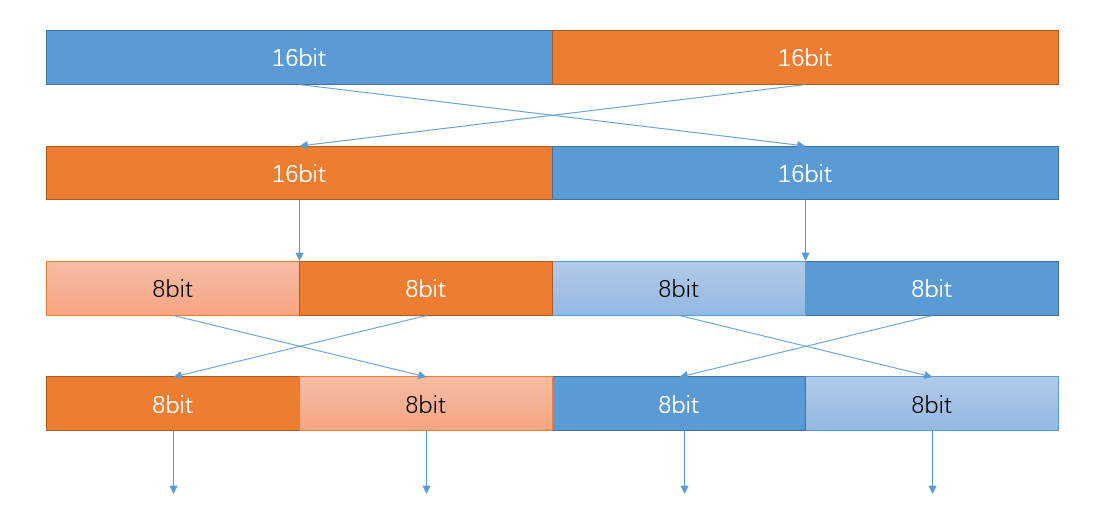
对于一个首尾对换的操作,我们可以使用分治的思路。
考虑对于最大的32位二进制,将前16位与后16位对换。
考虑高低的16位,将每一部分中的高8位与低8位对换。
如此进行······
那么,我们如何做到这种形式的对换呢?
不妨以8位二进制为例,对于一个八位二进制数
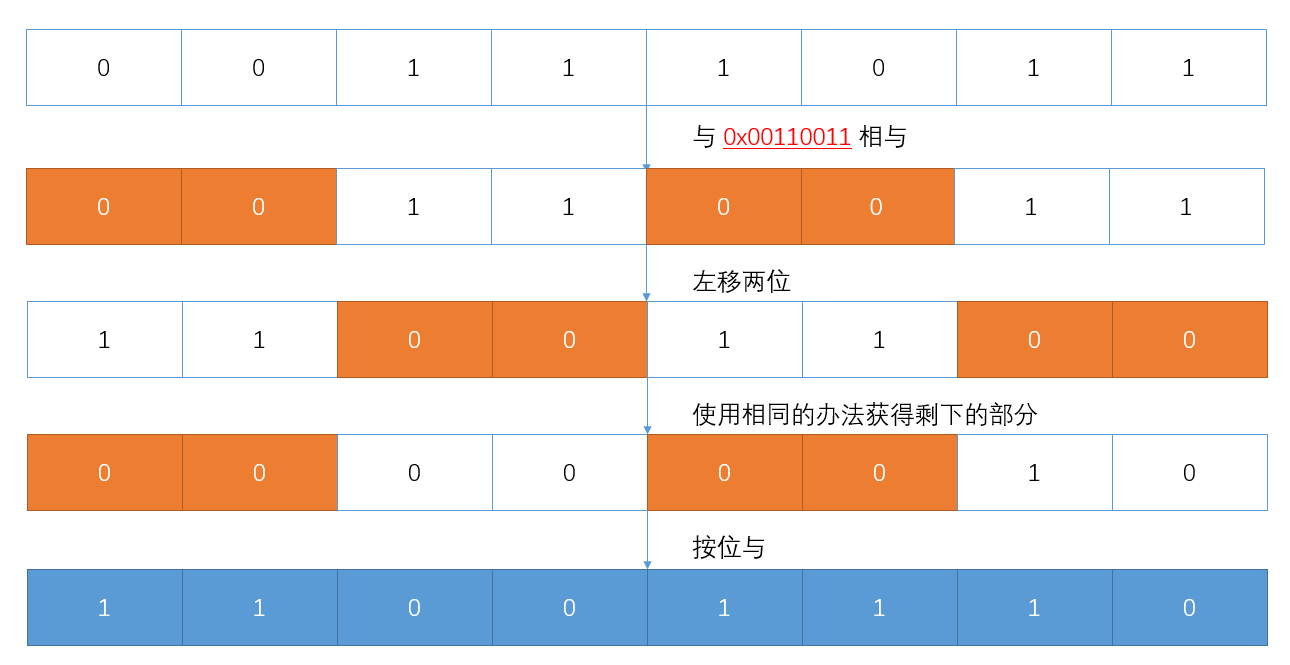
1011 0011,我们首先需要将其高低四位进行对换。示意如下:对于一个二进制数,我们可以很简单地使用如下办法取得它的高低四位:
highBits = 0x10110011 & 0x11110000 = 0x10110011 & 0xf0
lowBits = 0x10110011 & 0x00001111 = 0x10110011 & 0x0f然后根据图中所示,高四位移至低四位,低四位移至高四位,即分别采取右移和左移的办法:
lowerPart = highBits >> 4
upperPart = lowBits << 4最后一步就非常简单了,两部分按位取或即可:
final = lowerPart | upperPart如此一来,我们实现了高低四位的对换。
紧接着,对于两部分4位来说,每4位中需要进行高低二位的对换。示意如下:
在这里,我们的两部分分别可以表示如下:
final = higherPart | lowerPart = (origin & 0x33 << 2) | (origin & 0xcc >> 2)最后,在每一个二位中进行高低一位的对换,示意图略。
8位如此解决,16位当然也可,32位亦然。
AC代码1
class Solution {
public:
uint32_t reverseBits(uint32_t n) {
uint32_t res = 0;
// 注意此循环的条件
for (int i = 0; i < 31; i++)
{
res += (n & 1);
res = res << 1;
n = n >> 1;
}
res += (n & 1);
return res;
}
};
AC代码2
class Solution {
public:
uint32_t reverseBits(uint32_t n) {
// 注意!由于移位操作的优先级高于按位与,需要在与操作部分添加括号
n = ((n & 0xffff0000) >> 16) | ((n & 0x0000ffff) << 16);
n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8);
n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);
n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
return n;
}
};
参考资料
[1] 负雪明烛.「循环」与「分治」解法[EB/OL].2021-03-29