许久未在博客写技术向的文章了,虽说此篇也算不得非常技术,好歹沾点边,免得这博客成为个人荒废的见证。
按照《计算机图形学编程(使用OpenGL和C++)》这本书对OpenGL的学习终于触及了一些难啃的部分,这一周前几天花了点时间来领会球体的实现,今日又花了不少时间来领会环面,颇觉得环面的实现还是比球体难一些。值得一记。
一些背景
- 这本书的坐标系都是右手坐标系,z轴指向屏幕外
y轴
↑
|
|
O——→ x轴(右)
/
/
z轴(指向屏幕外)
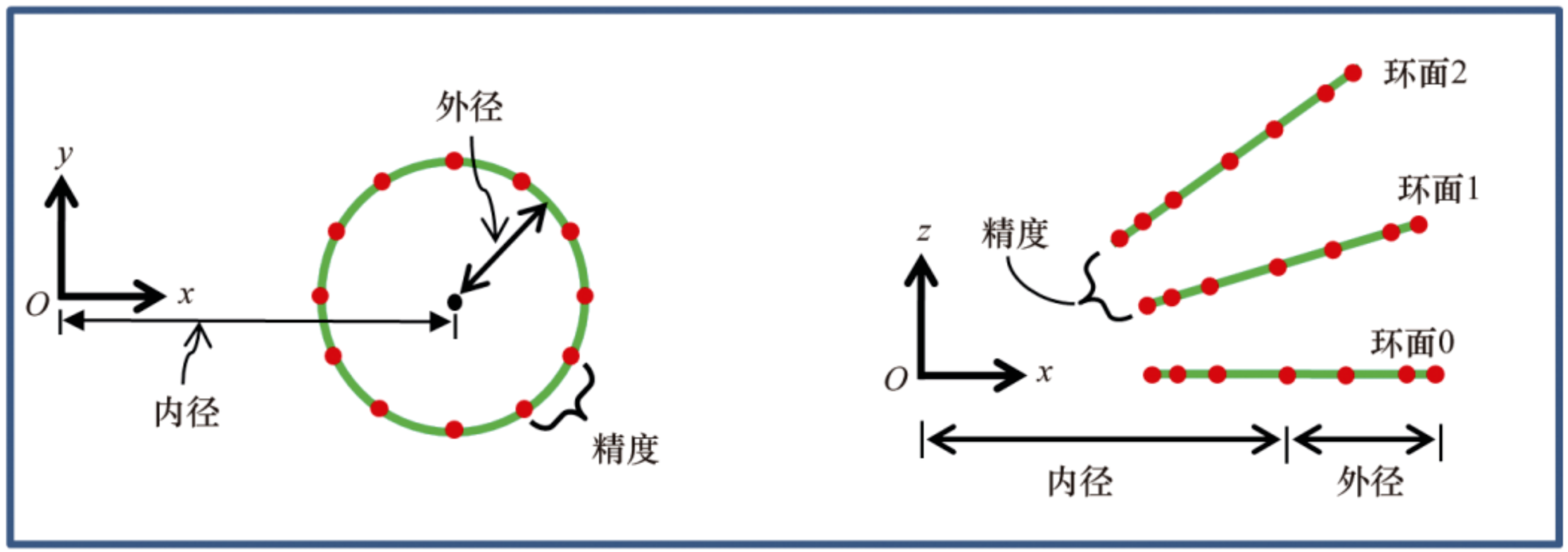
- 环面的内径和外径的定义如下图
- 总体思路是微积分,把环面视为一个位于xOy平面上的圆绕y轴旋转出来的,每次旋转微小的角度,形成环面。
实现
教程上的方法是基于旋转,悟到之后是不算难。
对于 Torus 类,提供一些常规的方法,供主函数使用:
#include <cmath>
#include <glm/glm.hpp>
#include <vector>
class Torus
{
public:
/**
* @brief Construct a new Torus object
* @param outerRadius Outer radius of the torus
* @param innerRadius Inner radius of the torus
* @param precision Precision of the torus
*/
Torus(float outerRadius, float innerRadius, uint16_t precision);
size_t GetIndicesCount() const;
size_t GetVerticesCount() const;
/** @brief Get the indices of the torus */
std::vector<uint16_t> GetIndices() const;
/** @brief Get the normals of the torus */
std::vector<glm::vec3> GetNormals() const;
/** @brief Get the texture coordinates of the torus */
std::vector<glm::vec2> GetTexCoords() const;
/** @brief Get the vertices of the torus */
std::vector<glm::vec3> GetVertices() const;
/** @brief Get the tangents of the torus (direction: y axis) */
std::vector<glm::vec3> GetSTangents() const;
/** @brief Get the tangents of the torus (direction: z axis) */
std::vector<glm::vec3> GetTTangents() const;
private:
uint16_t mPrecision{0U};
float mOuterRadius{.0f};
float mInnerRadius{.0f};
std::vector<uint16_t> mIndices;
std::vector<glm::vec3> mNormals;
std::vector<glm::vec2> mTexCoords;
std::vector<glm::vec3> mVertices;
std::vector<glm::vec3> mSTangents;
std::vector<glm::vec3> mTTangents;
private:
void Build();
};
旋转法构造环面的思路:
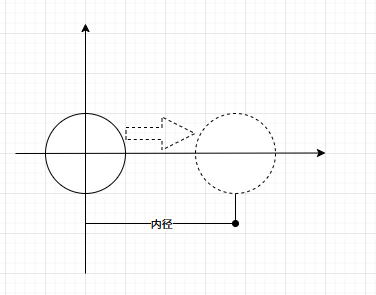
- 构建第0个环,位于XOY平面,它是由位于原点的圆平移内径距离得到的。原点上的圆的采样点本身又由
(outerRadius,0,0)绕z轴旋转得到。因此,对于精度mPrecision的环,第i个顶点就是(outerRadius,0,0)先绕z轴旋转angle、再向外平移innerRadius得到,其中angle就是i * 2π/mPrecision。
-
切向量随便找两条,按照教程上采用-y和-z叉乘得到法向量,然后跟着环旋转。目前法向量没啥用,但将来计算光照时会用到,所以不容出错。
-
对于纹理,这里的思路是把纹理水平伸展贴到环面上,类似于把一张长条形的包装纸贴到甜甜圈上,其中用包装纸短边包裹柱体。因此,对于XOY平面的纹理,只有y坐标需要赋值(根据采样精度来取点),x坐标是
0。
综上,第一个环如下构造:
for (uint16_t i = 0; i <= mPrecision; ++i)
{
float angle = 2.0f * glm::pi<float>() * i / mPrecision;
glm::mat4 rMat = glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f)); // 沿z轴转
glm::vec3 point = rMat * glm::vec4(mOuterRadius, 0.0f, 0.0f, 1.0f);
mVertices.emplace_back(point + glm::vec3(mInnerRadius, 0.0f, 0.0f)); // 旋转后平移,得出XOY平面上的圆的采样点
// 纹理坐标
mTexCoords.emplace_back(0.0, static_cast<float>(i) / mPrecision);
// 切向量
mTTangents.emplace_back(rMat * glm::vec4(0.0f, -1.0f, 0.0f, 1.0f));
mSTangents.emplace_back(0.0f, 0.0f, 1.0f);
// 法向量
mNormals.emplace_back(glm::cross(mTTangents.back(), mSTangents.back()));
}
对于第2~n个环,实际就是把第一个环沿y轴旋转,采样精度是 mPrecision 的情况下,每此旋转 2π/mPrecision 。切向量和法向量都和顶点一样直接拿第一个环的数据旋转。
纹理,要从x方向采样,因此纹理的x坐标每次增加 1/mPrecision 。
// 第2~n个环,沿y轴旋转第一个环得出
for (uint16_t ring = 1; ring <= mPrecision; ++ring)
{
float theta = 2.0f * glm::pi<float>() * ring / mPrecision;
glm::mat4 rMat = glm::rotate(glm::mat4(1.0f), theta, glm::vec3(0.0f, 1.0f, 0.0f));
// 第 ring 个环上第 i 个顶点
for (uint16_t i = 0; i <= mPrecision; ++i)
{
// 直接旋转第0个环的顶点
mVertices.emplace_back(rMat * glm::vec4(mVertices[i], 1.0f));
// 纹理水平展开
mTexCoords.emplace_back(static_cast<float>(ring) / mPrecision, static_cast<float>(i) / mPrecision);
// 切向量和法向量都直接旋转
mSTangents.emplace_back(rMat * glm::vec4(mSTangents[i], 0.0f));
mTTangents.emplace_back(rMat * glm::vec4(mTTangents[i], 0.0f));
mNormals.emplace_back(rMat * glm::vec4(mNormals[i], 0.0f));
}
}
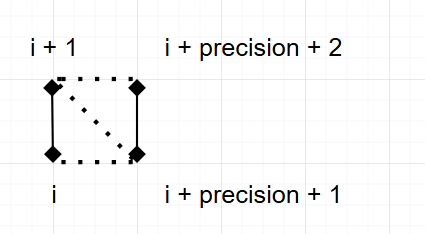
顶点索引,是指第 i 个三角形的三个顶点分别取用哪些点。本书的思路是取相邻环上的四个点,构成两个三角形。
这里的竖线可以理解为某个圆环的 侧视 ,环上的一点
i和它的邻点i + 1;隔壁环上与点
i处于同一水平线的一点,一定与当前的点i隔了precision + 1个点(因为每个环采样了precision + 1个点),因此是i + precision + 1和它的邻点i + precision + 2。
综上所述,按照旋转法构建的环面,核心代码如下:
void Torus::Build()
{
// 第一个环,XOY平面,构建第 i 个顶点
for (uint16_t i = 0; i <= mPrecision; ++i)
{
float angle = 2.0f * glm::pi<float>() * i / mPrecision;
glm::mat4 rMat = glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f)); // 沿z轴转
glm::vec3 point = rMat * glm::vec4(mOuterRadius, 0.0f, 0.0f, 1.0f);
mVertices.emplace_back(point + glm::vec3(mInnerRadius, 0.0f, 0.0f)); // 旋转后平移,得出XOY平面上的圆的采样点
// 纹理坐标
mTexCoords.emplace_back(0.0, static_cast<float>(i) / mPrecision);
// 切向量
mTTangents.emplace_back(rMat * glm::vec4(0.0f, -1.0f, 0.0f, 1.0f));
mSTangents.emplace_back(0.0f, 0.0f, -1.0f);
// 法向量
mNormals.emplace_back(glm::cross(mTTangents.back(), mSTangents.back()));
}
// 第2~n个环,沿y轴旋转第一个环得出
for (uint16_t ring = 1; ring <= mPrecision; ++ring)
{
float theta = 2.0f * glm::pi<float>() * ring / mPrecision;
glm::mat4 rMat = glm::rotate(glm::mat4(1.0f), theta, glm::vec3(0.0f, 1.0f, 0.0f));
// 第 ring 个环上第 i 个顶点
for (uint16_t i = 0; i <= mPrecision; ++i)
{
// 直接旋转第0个环的顶点
mVertices.emplace_back(rMat * glm::vec4(mVertices[i], 1.0f));
// 纹理水平展开
mTexCoords.emplace_back(static_cast<float>(ring) / mPrecision, static_cast<float>(i) / mPrecision);
// 切向量和法向量都直接旋转
mSTangents.emplace_back(rMat * glm::vec4(mSTangents[i], 0.0f));
mTTangents.emplace_back(rMat * glm::vec4(mTTangents[i], 0.0f));
mNormals.emplace_back(rMat * glm::vec4(mNormals[i], 0.0f));
}
}
for (uint16_t i = 0; i < mPrecision; ++i)
{
for (uint16_t j = 0; j <= mPrecision; ++j)
{
uint16_t first = i * (mPrecision + 1) + j;
uint16_t second = first + mPrecision + 1;
mIndices.emplace_back(first);
mIndices.emplace_back(second);
mIndices.emplace_back(first + 1);
mIndices.emplace_back(second);
mIndices.emplace_back(second + 1);
mIndices.emplace_back(first + 1);
}
}
}
而 main.cpp 中,初始化时就把环面的顶点数据传入VBO,其中索引数据通过 GL_ELEMENT_ARRAY_BUFFER 标识。
Torus torus { 0.5f, 1.0f, 48U };
void setupVertices(void)
{
auto vertices = torus.GetVertices();
auto normals = torus.GetNormals();
auto texCoords = torus.GetTexCoords();
auto indices = torus.GetIndices();
// 先生成并绑定VAO和VBO
glGenVertexArrays(1, vao);
glBindVertexArray(vao[0]);
glGenBuffers(numVBOs, vbo);
// 填充顶点位置数据
{
std::vector<float> vertexData;
for (auto& vertex : vertices)
{
vertexData.push_back(vertex.x);
vertexData.push_back(vertex.y);
vertexData.push_back(vertex.z);
}
glBindBuffer(GL_ARRAY_BUFFER, vbo[0]);
glBufferData(GL_ARRAY_BUFFER, vertexData.size() * sizeof(float), vertexData.data(), GL_STATIC_DRAW);
}
// 填充纹理坐标数据
{
std::vector<float> texCoordData;
for (auto& texCoord : texCoords)
{
texCoordData.push_back(texCoord.x);
texCoordData.push_back(texCoord.y);
}
glBindBuffer(GL_ARRAY_BUFFER, vbo[1]);
glBufferData(GL_ARRAY_BUFFER, texCoordData.size() * sizeof(float), texCoordData.data(), GL_STATIC_DRAW);
}
// 填充法线数据
{
std::vector<float> normalData;
for (auto& normal : normals)
{
normalData.push_back(normal.x);
normalData.push_back(normal.y);
normalData.push_back(normal.z);
}
glBindBuffer(GL_ARRAY_BUFFER, vbo[2]);
glBufferData(GL_ARRAY_BUFFER, normalData.size() * sizeof(float), normalData.data(), GL_STATIC_DRAW);
}
// 填充索引
{
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, vbo[3]);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, indices.size() * sizeof(uint16_t), indices.data(), GL_STATIC_DRAW);
}
}
【TODO】数学
yeah,环面和球面一样,也是有数学表达式的,感觉会比先构造第一个环、再旋转出第2~n个环优雅一些,不过可能要再考虑一下切向量和法向量怎么求得。todo……